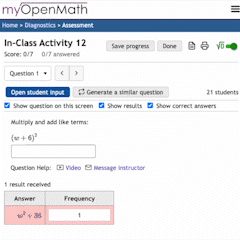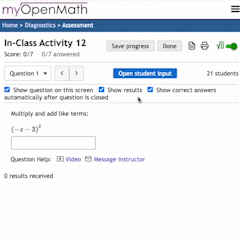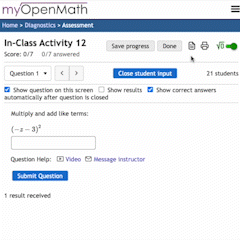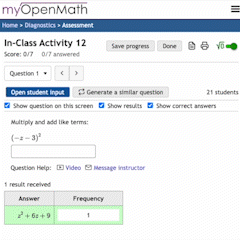
Rough Work
“Solve 2+2, Show your rough work.”
Being asked to “show your work”, “justify your answer”, or “write every step down” is a staple of education, and for good reason. For essays, a draft copy or outline can be used to find issues early on. In the sciences, and especially mathematics, rough work shows how you arrived at a solution.

What is Rough Work?
Rough work is the name we give to the steps you took to get to a solution. Rough work is a tool to organize your thinking, track your progress, and justify your final answer. No bridge is ever built where the engineer simply states “it can hold 30 tons, trust me” without the requisite 500 page report to back it up. Writing a technical report is the workplace equivalent of “show your work”. An academic paper is the same; a way to show your result, and how you got to it so others can “see for themselves”. Rough work is a reference to others so they can review your steps, check for mistakes and confirm your findings.
Why Show Your Work?
Try this. In your head, don’t write anything down or use calculator and solve this problem:
353
x432 Chances are you can comfortably do some of the calculation. But once you finish the next part you’ve forgotten the result of the first part. Your natural instinct is write down the first part. As the calculation becomes ever more complicated you have to write something down eventually. Perfect memory savants aside, doing rough work helps track long complex calculation.
Rough work is also for “Ah Ha!” moments. Sometimes in especially difficult problems what to do next doesn’t come to you immediately— it could take minutes, days or even years before a solution comes to you. Here the solution is now obvious to you, but late when you forget, the notes you took will be invaluable. Famously the mathematician Pierre de Fermat upon reading a particular problem wrote “I have discovered a truly marvelous proof of this, which this margin is too narrow to contain”. And died before he wrote it down in full. This problem ended up taking other mathematicians over 400 years to solve. The final solution is now contained in multiple papers and over hundreds of pages of proof. Fermat’s Last Theorem, as it’s called, still stands unsolved as a ”truely marvellous proof”. Don’t be Fermat; be a great mathematician, but show your work.
If you’re in school your professor probably requires rough work. No one plans to get the answer wrong, so requiring rough work helps to save you from yourself. While writing a test where you may need to write long complex calculations. It’s also good to leave a bread trail, chances are you won’t remember later exactly where that 42 came from during the test. Was it a clear comprehension error or was it a 24? So do write some rough work and sort out the typos later.
And of course if you cant get to a solution, rough work is at least something. Show what you do know and maybe get some credit for know something rather than nothing.
How Much Rough Work?
The type rough work for a problem is often tied to the level of understanding and knowledge that is expected. For instance, if the professor asks you to show work for 2+2, then perhaps you are just starting school and a diagram is needed. Your understanding might just be significantly ahead of the expected knowledge in the class. Maybe it is blindingly obvious to you that $\int _1^7 x^2 dx$ is 114, but probably not true of everyone in the class. The skill of explaining how you got to the answer is still helpful later when you approach more complex problems.

In some cases proving your answer can also be a good way to show your work. If you can “just know” that $x^2+5x+6$ is $(x+2)(x+3)$ then show the steps to expand your answer and show that indeed $(x+2)(x+3)=x^2+5x+6$. Rough work gives you a place to justify your answer, even for multiple choice. Explaining how you got an answer might be a way to show an alternative and perfectly valid solution.
How to Submit Digital Rough Work
For online tests and assignments submitting rough work is a little more than stapling your scrap paper to the test. A scanning app can quickly capture all of your rough work as a single file and make it easier for your professor to read. An app with a connected cloud storage service like the Microsoft Office App, OneDrive, Google Drive, or Files on iOS can scan documents to your cloud account then access them immediately on your computer.
Scanning your documents can also be a great way to archive your school work. At the end of the term it can be hard to part with all the papers youve written, because you “might need it later”. Scanning all of your work ensures you have access to it again later, and it doesn’t require 10 boxes in your attic.
So whether you’re filing a major report, solving a centuries old problem, or just writing a math test, add some rough work. It might help you organize your thoughts better and catch some errors, or you might look back on it with your prof and laugh, and gain a few more marks.